На днях благодаря очередному рассекреченному Эдвардом Сноуденом документу стало известно, что АНБ работает над созданием квантового компьютера.| Газета Washington Post осветила эту историю с довольно сенсационным заголовком: «АНБ стремится построить квантовый компьютер, способный взламывать большинство типов шифрования».
Естественно, это вызвало большое беспокойство среди новых поклонников Биткоин на Реддите и в Фейсбуке. На самом деле там не так уж много оказалось раскрыто, чего люди не знали или не ожидали. Общеизвестно, что АНБ и ранее спонсировало проекты создания квантовых компьютеров. Сам факт того, что внутри Агентства проект называется «Проникновение в труднодоступные цели» (Penetrating Hard Targets), новый, но не неожиданный. Мы узнали, что проект имеет бюджет в 79,7$ млн, но если честно, это не так уж много и, как заметила газета, документы не раскрывают, насколько далеко АНБ продвинулось в своих исследованиях. «Кажется маловероятным, чтобы АНБ существенно опережало в этом деле весь остальной мир, и никто об этом ничего не знал», — констатировали в Вашигтон Пост.
Тем не менее похоже, что сейчас самое подходящее время обсудить последствия внедрения квантовых вычислений в преломлении к будущему Биткоин.
Давайте начнем с маленького примера для тех, кто не знаком с квантовыми вычислениями. Современные компьютеры кодируют информацию в битах — бинарных числах 0 или 1. Эти биты обычно хранятся на жестком диске вашего компьютера. Их запись происходит путем изменения полярности намагниченности крошечных участков магнитного диска. Также биты хранятся в оперативной памяти или во флеш-памяти, где они представляют собой два различных уровня заряда в конденсаторе. Строки битов могут быть объединены для получения данных, которые могут быть прочитаны человеком. Например, строка 01000001 представляет собой букву «А» в расширенной таблице ASCII. Любые расчеты с битами выполняются последовательно, один за другим.
 Фотонно-квантовые компьютеры используют различные состояния квантовых частиц, представляющих собой квантовые биты, сокращенно кубиты. Например, фотон, вращающийся в вертикальной плоскости, может быть 1, а в горизонтальной плоскости — 0. Наряду с этим фотоны могут существовать в довольно странном состоянии, называемом суперпозицией. То есть наряду с тем, что они могут вращаться в вертикальной, горизонтальной и диагональных плоскостях по отдельности, они также могут вращаться во всех этих направлениях одновременно. Даже не спрашивайте, как это возможно, это магия мира квантовой механики.
Фотонно-квантовые компьютеры используют различные состояния квантовых частиц, представляющих собой квантовые биты, сокращенно кубиты. Например, фотон, вращающийся в вертикальной плоскости, может быть 1, а в горизонтальной плоскости — 0. Наряду с этим фотоны могут существовать в довольно странном состоянии, называемом суперпозицией. То есть наряду с тем, что они могут вращаться в вертикальной, горизонтальной и диагональных плоскостях по отдельности, они также могут вращаться во всех этих направлениях одновременно. Даже не спрашивайте, как это возможно, это магия мира квантовой механики.
С практической точки зрения это означает, что в один момент времени обычный компьютер выполняет всего одно вычисление, в то время как квантовый может совершать миллионы калькуляций, повышая таким образом компьютерную производительность в миллионы раз.
Теперь когда журналисты пишут нечто вроде: «В металлических ящиках размером с комнату, защищенных от электромагнитных утечек, АНБ строит компьютер, который сможет взломать почти любой тип шифрования, используемый для защиты банковских, медицинских и правительственных данных по всему миру», — это, естественно, заставляет людей думать, что той криптографии, какой мы ее знаем сегодня, пришел конец. Но это не наш случай.
Давайте рассмотрим тот тип атаки, который приходит на ум большинству людей, когда они слышат о квантовых компьютерах — брутфорс. Это когда вы последовательно перебираете все ключи, пока не найдете нужный. Обладая достаточным количеством времени, вы можете подобрать любой ключ. Проблема в том, что для взлома достаточно длинного ключа шифрования обычному компьютеру потребуются миллиарды, а то и триллионы лет. Но, конечно, квантовые компьютеры могут с этим справиться, верно? Цитата из книги Брюса Шнейера «Прикладная криптография», написанной в 1996 году:
Один из выводов из второго закона термодинамики таков: для представления информации нужно определенное количество энергии. Для записи одного бита путем смены состояния системы требуется энергии не меньше, чем kT, где Т есть абсолютная температура системы, а k — постоянная Больцмана (не расходитесь, урок физики почти закончился).
Учитывая, что k = 1.38×10^(-16) эрг/° Кельвина, а температура вселенной равна 3.2° Кельвина, идеальный компьютер, работающий при температуре 3.2°K будет потреблять 4.4×10^(-16) эрг каждый раз при смене бита. Для того, чтобы компьютер работал при температуре холоднее, чем космическая радиация, потребуется дополнительная энергия для запуска теплового насоса.
Далее, годовой объем энергии, выделяемой нашим Солнцем, примерно составляет 1.21×10^41 эрг. Этого достаточно для 2.7×10^56 изменений битов в нашем идеальном компьютере, то есть для того, чтобы прокрутить 187-разрядный счетчик от нуля до максимума. Если бы мы построили сферу Дайсона вокруг Солнца и удерживали бы всю его энергию без потерь в течение 32 лет, наш компьютер досчитал бы до 2^192. Правда, при этом на выполнение каких-либо более полезных операций энергии бы уже не осталось.
Но это только одна звезда, причем далеко не самая массивная. Типичная сверхновая излучает порядка 10^51 эрг. В форме нейтрино излучение в сотню раз больше, но мы их не трогаем, пусть себе летят. Если бы вся эта энергия могла бы быть собрана воедино в неистовой вычислительной оргии, мы бы смогли прокрутить от начала до конца 219-битный счетчик.
Эти цифры не имеют ничего общего с технологией устройств, просто это тот максимум, который позволяет достичь термодинамика. Кроме того, они означают, что брутфорс, направленный на 256-битные ключи, невозможен, пока компьютеры не построены из чего-то другого, чем материя, и не занимают нечто иное, чем пространство.
Повторим еще раз. Даже если вы соберете всю энергию от сверхновой воедино и направите ее в идеальный компьютер, вы все равно не сможете взломать простым перебором обычный ключ шифрования. Следовательно, если вы собираетесь взламывать коммерческие коды, вы должны атаковать математику, лежащую в основе алгоритма шифрования.
Сегодня большинство алгоритмов шифрования с открытым ключом опираются либо на трудности целочисленной факторизации (RSA), либо на задачи дискретных логарифмов (DSA/El Gamal и криптография эллиптических кривых). В 1994 году математик Питер Шор (Peter Shor) продемонстрировал эффективный квантовый алгоритм для факторинга и вычисления дискретных логарифмов, который мог бы взламывать шифры с открытыми ключами, если бы использовался на квантовом компьютере. Правда, он может взломать далеко не все типы кодирования. Традиционная криптография с симметричным ключом и криптографические хеш-функции все равно будут лежать далеко за пределами поля зрения квантовых алгоритмов.
Влияние на Биткоин
В Биткоин используется несколько алгоритмов шифрования: алгоритм цифровой подписи эллиптических кривых (ECDSA) для подписи транзакций и хеш-функции SHA-256 и RIPEMD160. Если АНБ сможет разработать квантовый компьютер, пригодный для взлома шифров, то ему удастся преодолеть ECDSA, однако SHA-256 и RIPEMD160 устоят.
Хорошая новость в том, что в случае признаков взлома ECDSA его достаточно легко заменить на другой тип шифрования. Было бы гораздо хуже, если бы в опасности оказался SHA-256. Если вы не знакомы с механикой Биткоин, напомним, что SHA-256 используется при майнинге. На данный момент миллиарды долларов были потрачены на компьютерные чипы, которые не выполняют ничего другого, кроме вычислений SHA-256. В случае уязвимости алгоритма SHA-256 всё это железо превратится в дорогое пресс-папье. Если бы такое произошло внезапно (в отличие от плавного перехода на другую хеш-функцию), это стало бы катастрофой. Безопасность сети Биткоин опирается на тот факт, что контролировать 51% вычислительных мощностей сети слишком сложно и дорого для злоумышленника. Внезапный переход на другую хеш-функцию создаст значительную угрозу безопасности и, скорее всего, вызовет обвал цен на биткоины. Но как уже говорилось, майнеры могут спать спокойно: квантовые компьютеры алгоритму SHA-256 не страшны. Хотя это не означает, что никто не сможет найти брешь для атаки в будущем.
Вернемся к ECDSA. Этот алгоритм генерирует пару ключей, один из которых открытый, а другой — закрытый. В Биткоин вы храните приватный ключ у себя и используете его для подписи транзакций, доказывая сети, что у вас есть биткоины, связанные с определенным адресом. Сеть проверяет вашу подпись, используя соответствующий открытый ключ. Работающий квантовый компьютер позволит АНБ отделить закрытый ключ от открытого. Значит ли это, что АНБ сможет украсть биткоины у каждого? Не совсем так.
Дело в том, что в Биткоин ваш открытый ключ (изначально) не является открытым. Пока вы не делитесь адресом вашего кошелька с другими, чтобы они смогли прислать вам монетки, ваш адрес — это только хеш-функция открытого ключа, а не сам ключ. Другими словами, хеш-функция — это односторонняя криптографическая функция, которая берет данные на входе и возвращает их в зашифрованном виде на выходе. Обратный процесс невозможен. Под односторонней функцией понимается то, что после операции хеширования вы уже не сможете отделить входные данные от того, что получилось на выходе. Так же, как если бы вы что-то зашифровали, а потом потеряли ключ. Для демонстрации давайте посчитаем RIPEMD160 хеш-функцию фразы «Hello World».
Hello World ==> a830d7beb04eb7549ce990fb7dc962e499a27230
Адрес кошелька Биткоин высчитывается из вашего открытого ключа путем запуска нескольких хеш-функций подряд вот таким образом:
Все написанное здесь — замысловатый способ показать вам, что злоумышленник с квантовым компьютером, даже отделив закрытый ключ от открытого, не сможет получить открытый ключ из адреса биткоин-кошелька, потому что он пропущен через несколько односторонних квантовоустойчивых хеш-функций.
Тем не менее для совершения транзакции вы должны транслировать в сеть свой открытый ключ — нет другого способа проверить вашу подпись. Это означает, что в страхе перед квантовым компьютером АНБ все Биткоин-адреса должны являться одноразовыми. Всякий раз, проводя транзакцию, вы должны переслать все лишние биткоины на вновь созданный адрес. Если вы не удалите весь баланс с вашего адреса, АНБ сможет украсть остаток. Это неудобно, но даст разработчикам достаточно времени, чтобы поменять ECDSA на квантовоустойчивую схему цифровой подписи.
Постквантовые цифровые подписи
Этот раздел будет немного техническим, но не особо сложным даже для начинающих. Существует несколько типов постквантовых систем шифрования с открытыми ключами: на основе теории решеток, кодов исправления ошибок, многомерных квадратичных схем и хеш-функций. Как уже упоминалось, криптографические хеш-функции предполагаются квантовоустойчивыми. При этом условии возможноа замена схемы цифровой подписи для ECDSA с использованием только хеш-функций. Давайте посмотрим на эти хеш-системы, так как они просты для понимания и основаны на уже широко использующихся хеш-функциях.
Схема одноразовой подписи Лэмпорта (LOTSS)
Для начала, чтобы обеспечить адекватную защиту, мы должны использовать хеш-функцию с как минимум 160-битным выходом. RIPEMD160 или SHA-1 должны подойти для этого. Чтобы сгенерировать пару открытый/закрытый ключ, мы начнем с генерации 160 пар случайных чисел. Этот набор случайных чисел будет закрытым ключом.
| Пара № | Открытый ключ |
|---|---|
| 1 | e9e515b332cf1ce01299497e9e94b7df353ff022 ce56dcfdb7038e6ab0b37c383dbfda8cb45d60ea |
| 2 | 811f71c5cf7639a40df7b9b187bf768016791cf8 1094b13455a133d2d11898cfa30916e12be3e0ab |
| … | |
| 159 | bc6a1eb98148850dd2b32ae632005f5472c06a70 c10f4ac3d645d891d9b5dc0fa0b7294ad14ac3df |
| 160 | 585801c9da7ce0d562f375338b456ba9f10be3f6 3c3363ed7273f1ef9c1aed3fc5a7433002b668f8 |
Для генерации открытого ключа мы возьмем хеш-функцию RIPEMD160 каждого из 320 чисел.
| Пара № | Закрытый ключ | Открытый ключ |
|---|---|---|
| 1 | e9e515b332cf1ce01299 ce56dcfdb7038e6ab0b3 |
d7c3e127380fbbbe37b9 4ddf29fb200aa0fd90b1 |
| 2 | 811f71c5cf7639a40df7 1094b13455a133d2d118 |
f84a8e5a0dce682e48c5 4a88310f694329b9ab97 |
| … | ||
| 159 | bc6a1eb98148850dd2b3 c10f4ac3d645d891d9b5 |
7d5c0e19c4dc9077be6c ffbbe97612e581f073b6 |
| 160 | 585801c9da7ce0d562f3 3c3363ed7273f1ef9c1a |
38ed36c30ee72c95c598 a546f885e8210c61767d |
Теперь, чтобы подписать сообщение подписью Лэмпорта, мы сперва сделаем каталог сообщений путем их хеширования с помощью RIPEMD160 (в Биткоине мы бы хешировали транзакцию), а потом сконвертируем то, что вышло, в бинарный вид. Попробуем в качестве примера опять использовать фразу «Hello World»:
Hello World ==> a830d7beb04eb7549ce990fb7dc962e499a27230 ==> 101010000011000011010111101111101011000001001110101101110101
01001001110011101001100100001111101101111101110010010110
00101110010010011001101000100111001000110000
Далее мы сопоставим каждую двоичную цифру с каждой парой нашего закрытого ключа. Если бит 0 — мы добавляем первое число пары к нашей подписи, если 1 — второе число.
| Пара № | Каталог | Закрытый ключ | Подпись |
|---|---|---|---|
| 1 | 1 | e9e515b332cf1ce01299 ce56dcfdb7038e6ab0b3 |
ce56dcfdb7038e6ab0b3 |
| 2 | 0 | 811f71c5cf7639a40df7 1094b13455a133d2d118 |
811f71c5cf7639a40df7 |
| … | |||
| 159 | 0 | bc6a1eb98148850dd2b3 c10f4ac3d645d891d9b5 |
bc6a1eb98148850dd2b3 |
| 160 | 0 | 585801c9da7ce0d562f3 3c3363ed7273f1ef9c1a |
585801c9da7ce0d562f3 |
Наконец, чтобы проверить, является ли подпись действительной, мы опять сперва создаем каталог сообщений, используя описанный выше процесс, затем хешируем каждое из 160 чисел в подписи с помощью RIPEMD160 и, наконец, проверяем, совпадают ли эти хеши с хешами открытого ключа, представленными в каталоге сообщений.
| Пара № | Хеш подписи | Каталог | Открытый ключ |
|---|---|---|---|
| 1 | 4ddf29fb200aa0fd90b1 | 1 | d7c3e127380fbbbe37b9 4ddf29fb200aa0fd90b1 |
| 2 | f84a8e5a0dce682e48c5 | 0 | f84a8e5a0dce682e48c5 4a88310f694329b9ab97 |
| … | |||
| 159 | 7d5c0e19c4dc9077be6c | 0 | 7d5c0e19c4dc9077be6c ffbbe97612e581f073b6 |
| 160 | 38ed36c30ee72c95c598 | 0 | 38ed36c30ee72c95c598 a546f885e8210c61767d |
Вот и получили, что хотели — квантовоустойчивую схему цифровой подписи, используя только хеш-функции. Только лицо, владеющее всеми 320 числами в закрытом ключе, сможет сгенерировать подпись, которая хеширует открытый ключ при сравнении с каталогом. Однако хотя эта схема фактически рабочая, она не без проблем. Во-первых, как следует из названия, подпись по методу LOTSS можно использовать только один раз. Причина в том, что вы в каждой подписи выкладываете по сути половину своего закрытого ключа. При таком раскладе, если подписывать несколько сообщений, то закрытый ключ будет полностью скомпрометирован. Применительно к Биткоин такую схему также можно было бы использовать только один раз.
Еще одна проблема в том, что размеры ключей и сигнатур получились абсурдно большими. Закрытый и открытый ключ суммарно весят 6400 байтов (сравните с 32 и 64 байтами для ключей с использованием алгоритма ECDSA). Аналогично, полученная нами подпись занимает 3200 байтов (71-73 байта при ECDSA). Биткоин уже имеет проблемы с масштабированием, и такое увеличение размеров ключей и подписей только усугубит их.
Закрытый ключ Лэмпорта может быть сильно уменьшен в размерах путем генерации случайных чисел из одного случайного источника (seed). Чтобы сделать это, нужно просто взять RIPEMD160 (seed + n), где n начинается с 1 и при каждой итерации увеличивается на единицу, пока не достигнет 320. К сожалению, размер закрытого ключа — не такая большая проблема, как размер открытого ключа и подписи. Есть еще одна схема одноразовой подписи, называемая подписью Винтернитца, в которой размера ключа может быть уменьшен, но это происходит за счет хеш-операций. К счастью, мы еще не закончили.
Схема подписи Меркля (MSS)
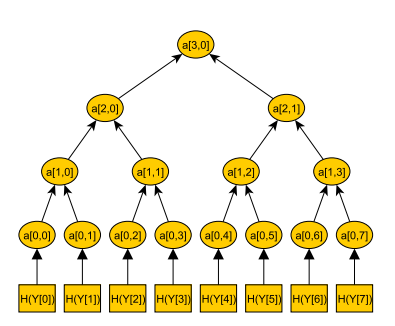
Схема подписи Меркля совмещает схему одноразовых подписей (либо Лэмпорта, либо Винтернитца) с деревом Меркля, также называемым деревом хешей. Такой подход позволяет подписывать одним открытым ключом много сообщений, не беспокоясь о безопасности. Давайте посмотрим, как это работает.
Мы начнем с создания ряда пар ключей Лэмпорта. Их количество будет равно количеству подписей, которые мы хотим получить из одного открытого ключа. В качестве примера возьмем, например, восемь. Затем вычислим дерево Меркля, используя каждый из восьми открытых ключей Лэмпорта. Для этого открытые ключи разбиваются на пары, хешируются, затем полученные хеши объединяются путем конкатенации и итоговые результаты снова хешируются. Этот процесс, похожий на замешивание теста, повторяется, пока не выйдет единый ком.
Хеш на самой вершине дерева (корень Меркля) — это открытый ключ Меркля. Такой способ значительно уменьшает размер открытого ключа с 6400 (в случае подписи Лэмпорта) до 20 байтов, то есть до длины одного RIPEMD160 хэша. Для расчета подписи надо выбрать одну пару ключей Лэмпорта и подписать сообщение точно так же, как мы делали это выше. Но в этот раз подпись будет состоять из подписи Лэмпорта и каждого листа дерева Меркля, ведущего от открытого ключа к корню.
На диаграмме выше подпись будет такой:
sig′||H(Y[i=2])||A[0]||auth[0]||A[1]||auth[1]||A[2]||auth[2]||A[3]
Для верификации подписи Меркля достаточно проверить подпись Лэмпорта, а затем убедиться, что листья хешируются в открытый ключ Меркля. Если все так, подпись действительна.
Итак, какие есть преимущества MSS над LOTSS? Во-первых, открытый и закрытый ключи весят 20 байтов вместо 6400. Во-вторых, к одному открытому ключу можно сделать множество подписей, правда, здесь есть немалая проблема. Чем больше сообщений вы хотите подписать своим открытым ключом, тем больше должно быть дерево Меркля. Чем больше дерево, тем больше подпись. В итоге подпись может стать такой большой, что ее использование окажется непрактичным, особенно в случае с Биткоин. Это приводит нас к последней постквантовой схеме подписи, которую мы сейчас и обсудим.
CMSS и GMSS
 Схема подписи Меркля известна уже более 30 лет, и несмотря на развитие криптоанализа ее ценность для шифрования не была опровергнута. Тем не менее в последние пять лет ее неоднократно пытались улучшить, что привело к интересным результатам. Так, появились Улучшенная (CMSS) и Обобщенная (GMSS) схемы подписи Меркля. Оба стоящих за этими схемами криптографа являются авторами книг по постквантовой криптографии.
Схема подписи Меркля известна уже более 30 лет, и несмотря на развитие криптоанализа ее ценность для шифрования не была опровергнута. Тем не менее в последние пять лет ее неоднократно пытались улучшить, что привело к интересным результатам. Так, появились Улучшенная (CMSS) и Обобщенная (GMSS) схемы подписи Меркля. Оба стоящих за этими схемами криптографа являются авторами книг по постквантовой криптографии.
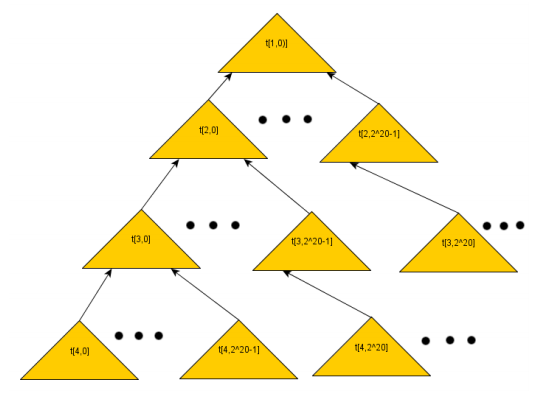
Обе схемы предлагают существенное увеличение количества подписей на один открытый ключ с сохранением разумной длины подписи и временем ее верификации. GMSS, в частности, предлагает практически неограниченное количество подписей — 2^80, но при этом показывает несколько меньшую производительность по сравнению с CMSS. Обе схемы решают задачу, разбивая систему на отдельные деревья Меркля с 2^n листьями. Подписью корневого дерева подписывается открытый ключ дерева ниже, которое в свою очередь также является подписью к дереву под ним, и так далее.
Таким образом, весьма вероятно, что какая-то из этих схем подписи станет серьезным кандидатом на замену ECDSA в Биткоин в постквантовом мире. Но почему бы нам самим не пойти дальше и попробовать реализовать его сейчас, вместо того, чтобы ждать, пока нас всех удивит АНБ? Давайте сделаем небольшое сравнение и посмотрим на скорость операции и размеры подписей для каждой схемы. Варианты CMSS имеют емкость хранения подписей 2^20, 2^30 и 2^40, в то время как для GMSS она составляет 2^40 и 2^80. Скорее всего, и 2^30 подписей было бы достаточно для Биткоин, потому что трудно себе представить кого-то, кто может сделать больше миллиарда или триллиона транзакций с одного кошелька. Еще схема GMSS может быть оптимизирована для более быстрой верификации, правда, ценой увеличения размера подписи на 25%.
| Размер закрытого ключа | Размер открытого ключа | Размер подписи | Время генерации | Время создания подписи | Время верификации | |
|---|---|---|---|---|---|---|
| ECDSA | 32 байта | 64 байта | 71-73 байта | 9.6 мс | 100 мс | 8.53 мс |
| CMSS20 | 1900 байт | 46 байт | 2128 байт | 4.1 сек | 12.5 мс | 2.0 мс |
| CMSS30 | 2788 байт | 46 байт | 2328 байт | 2 мин | 17.0 мс | 2.0 мс |
| CMSS40 | 3668 байт | 46 байт | 2528 байт | 62.3 мин | 21.7 мс | 2.0 мс |
| GMSS40 | 1640 байт | 20 байт | 1860 байт | 723 мин | 26.0 мс | 19.6 мс |
| GMSS40′ | 1680 байт | 20 байт | 2340 байт | 390 мин | 10.7 мс | 10.7 мс |
Из таблицы видно, что CMSS и GMSS фактически работают лучше, чем ECDSA, в отношении размера открытого ключа и времени подтверждения подписи. Однако в критичных вещах, которые влияют на масштабируемость и размер подписи, они хуже. Время верификации для CMSS на самом деле лучше чем у ECDSA, что должно улучшить масштабируемость, а оптимизированный вариант GMSS также находится весьма близко к желаемым значениям. Тем не менее размер подписи для обеих схем остается существенной проблемой. Давайте проведем грубую оценку.
Сейчас размер транзакции — около 500 байтов. Оба варианта — и CMSS, и GMSS — увеличат транзакцию до 4 килобайт. Это означает увеличение размера блока в цепочке на 700%. Вся цепочка блоков на сегодняшний день превышает 13 гигабайт. Если бы Биткоин использовал эти схемы подписей с самого начала, то уже сейчас цепочка «весила» бы более 100 гигабайт. Подпись и размер ключа являются проблемой не только для описанных схем, остальные находятся в той же ловушке.
Стоит обратить внимание также и на сумасшедшее время генерации ключа у GMSS. Если вы оставите компьютер включенным на сутки, вы сможете сгенерировать всего три кошелька, и это используя оптимизированный вариант с увеличенными размерами подписей. Хотя подозреваю, что оборудование ASIC значительно ускорило бы время генерации кошельков. У CMSS с этим не все так плохо.
Другими словами, Биткоин не может сейчас перенять ни одну из этих схем подписи, если он хочет продолжать масштабироваться. Однако с течением времени квантовые компьютеры становятся все более жизнеспособными, а закон Мура скорее всего доведет стоимость хранения и вычислительную мощность до той точки, когда CMSS, GMSS или какой-нибудь другой тип постквантовой подписи сможет быть внедрен в Биткоин. До тех пор давайте не забывать об АНБ и его проекте «Проникновение в труднодоступные цели».
Источник: BitcoinNotBombs








Дело в другом. Предположим, АНБ скомпрометировала весь Биткоин. Весь. Все рухнуло. НО ИДЕЯ ОСТАЛАСЬ. И понятна ее реализация. Просто из 70 валют выживет более устойчивая к взлому.
АНБ это невыгодно. Поэтому они не будут это делать, а будут ограничиваться отдельными кошельками, и в основном хакерскими методами.
Компрометация всей системы возможна лишь в случае войны.
В статье к законам квантового мира применено следствие из закона макромира -термодинамики, что неверно. Но 79 млн. долл. на разработку все равно не хватит, оценочная цифра — 10 млрд и 20 лет времени.
Таких запугивающих новостей, будет ещё не мало! Вся массмедиа спустит палкана на биткоин и они пойдут на это, в любом случае. Запугивания и ложь — это их конёк, чтобы удержать власть над деньгами! Вопрос в том: «кто испугается и поведётся на провокацию?!»